Union & Find
union & Find 이라는 알고리즘은 Union과 Find으로 이루어져있다.
Union은 합치기
Find는 찾기
두 집합이 같은 집합에 있는지 확인하기위해 트리를 사용해서 하나의 집합에 있는지 확인하는 방법이다.
예를들어 A라는 집합에 1 3 5 7 9가있고 B라는 집합엔 2 4 6 8이 있다.
그리고 1 2 3 4 5 6 7 8 9중에 랜덤한 두 수가 같은 집합인지 물어본다고 한다.
1 5는 같은 집합인가요? 네
2 6은 같은 집합인가요? 네
1 8은 같은 집합인가요? 아니오
이런 방법을 판별하기 위해 for문으로 1~9까지 반복한다면 O(N)이 나온다.
하지만 Union & Find로 판별한다면 트리의 높이만큼 탐색할 때와 같이 O(logN)이 나온다.
Union & Find는 구현하기위해 각 집합을 트리로 구현하며 최상위 부모가 최솟값이 되어야 한다.
즉, 올라갈수록 더 작은값이 되어야 한다.
물론 최대값으로 만들어도 상관없지만 일방적으로 최솟값이 되도록 구현한다.
사용법
Union & Find에서 중요한 것은 Find이다.
Find는 현재 트리에서 최상위 부모(최솟값)을 찾는 과정이다.
파이썬의 구현 코드
def find(x):
if parent[x] != x:
return find(parent[x])
return x재귀함수를 활용해서 부모를 찾으면 된다.
Union은 두 개의 트리를 합하는 방법이다.
파이썬의 구현 코드
def union(a,b):
x = find(a)
y = find(b)
if x < y: parent[y] = x
else: parent[x] = ya라는 트리와 b라는 트리의 부모를 찾는다.
두 트리중 부모의 값이 더 작은 값쪽으로 트리를 붙인다.
1~9까지 수를 짝수와 홀수로 나눠서 무작위로 입력한다고 가정하자.

위 그림에서 짝수와 홀수로 구분지어서 합하기 위해 순서대로 입력이 들어오면 합친다고 한다.
1 3

9 7

7 3

1 5
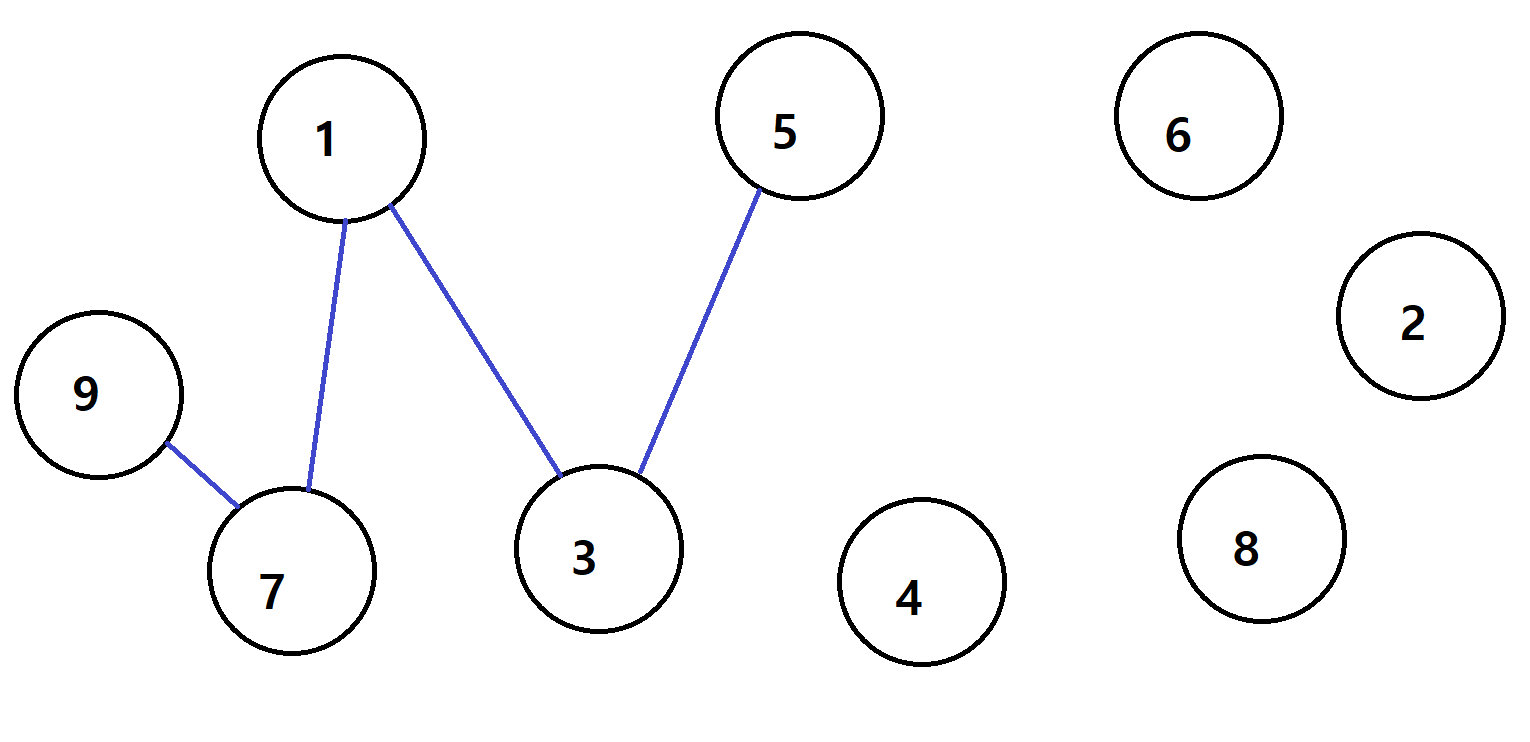
이렇게 홀수가 만들어졌다고 하자.
그리고 짝수는
8 6
6 4
4 2
의 순서로 입력이 들어와서 이렇게 구현되었다고 하자.
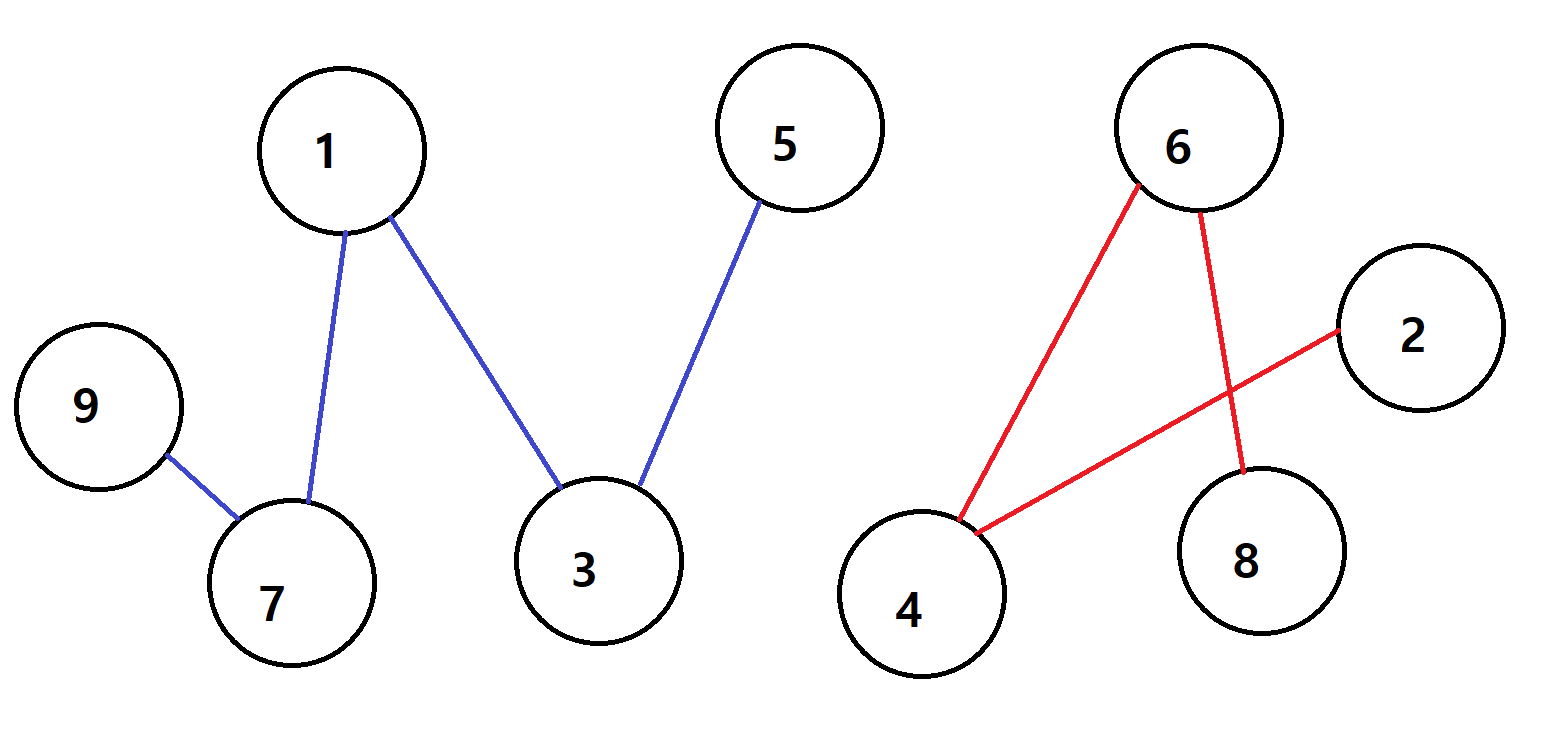
이러면 확실하게 부모노드가 1과 2로 구분되어져서 두 집합이 구분되어 있는게 보인다.
하지만 이렇게만 구현한다면 경로 압축이 되지않아서 최악의 경우 O(2N)의 탐색을 해야할 수도 있다.

9 8
8 7
7 6
...
3 2
2 1
으로 입력이 주어진 경우다.
부모를 탐색하기위해 9의 부모를 찾으려면 1까지 올라갔다가 내려와야한다.
이를 위해 경로탐색을 해줘야 한다.
경로 압축
어려워 보이지만 별로 어려울게 없다.
Find에서 한줄만 더 적으면 된다.
def find(x):
if parent[x] != x:
parent[x] = find(parent[x])
return parent[x]
return x
Find에서 부모노드를 찾으면서 최상위 부모에 등록을 해버리는 방법이다.
이러면 경로가 압축되기 때문에 탐색 시간을 단축시킬 수 있다.
추가 문제
https://www.acmicpc.net/problem/1717
1717번: 집합의 표현
첫째 줄에 n(1 ≤ n ≤ 1,000,000), m(1 ≤ m ≤ 100,000)이 주어진다. m은 입력으로 주어지는 연산의 개수이다. 다음 m개의 줄에는 각각의 연산이 주어진다. 합집합은 0 a b의 형태로 입력이 주어진다. 이는
www.acmicpc.net
참고 링크
https://gmlwjd9405.github.io/2018/08/31/algorithm-union-find.html
[알고리즘] Union-Find 알고리즘 - Heee's Development Blog
Step by step goes a long way.
gmlwjd9405.github.io
https://www.youtube.com/watch?v=AMByrd53PHM&t=378s
'백준 > 이론_python' 카테고리의 다른 글
| 문자열 뒤집기 python (0) | 2023.04.11 |
|---|---|
| 나머지 분배법칙(모듈러 연산) (0) | 2023.02.11 |
| 백준의 long과 int의 차이 (0) | 2023.02.11 |
| 비트 마스킹 C++ (0) | 2023.01.17 |
| 분할 정복 알고리즘 python (0) | 2023.01.16 |

댓글